👨🏼‍⚕️ The Most Important Statistics Question That You Should Memorize

Doctor's Offices vs Math

I recently had my first visit to a primary care doctor in over 10 years.

I'm a relatively healthy young person and the more I've learned about statistics and decision making under uncertainty, the less comfortable I've become with doctor's offices.

However, despite my skepticism, I sought out a primary care doctor because I think understanding biomarkers from your bloodwork is important - and I'm kind of wasting my health insurance if I don't do these checkups at least annually.

We got to talking and got on the topic of risks and medicines and I was told something along the lines of: "If X medicine increases your chance of avoiding disease by 30% then why wouldn't you take the 30% increase in your health?"

In my opinion, a college level understanding of statistics is important for every professional who is making life altering decisions

With that said, let's take a look at the classic Bayes' Theorem statistics problem that every doctor (and really every professional) should know by heart:

A patient goes to see a doctor. The doctor performs a test with 99 percent reliability--that is, 99 percent of people who are sick test positive and 99 percent of the healthy people test negative. The doctor knows that only 1 percent of the people in the country are sick. Now the question is: if the patient tests positive, what are the chances the patient is sick?

Intuitively, the answer is very simple.

If 99% of the people who are sick test positive, the answer is the patient is 99% likely to be sick.

This is, however, incorrect.

We have to apply Bayes' Theorem because we have prior knowledge of the patient population.

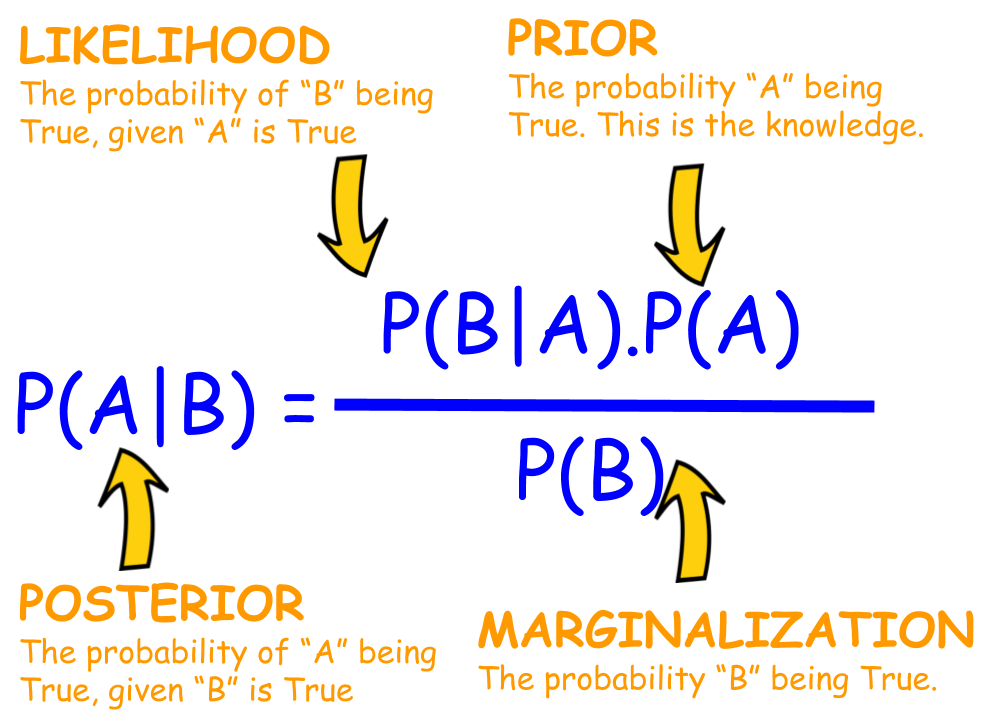
To find out our P(A), P(B), and P(B|A) we need to do a little math

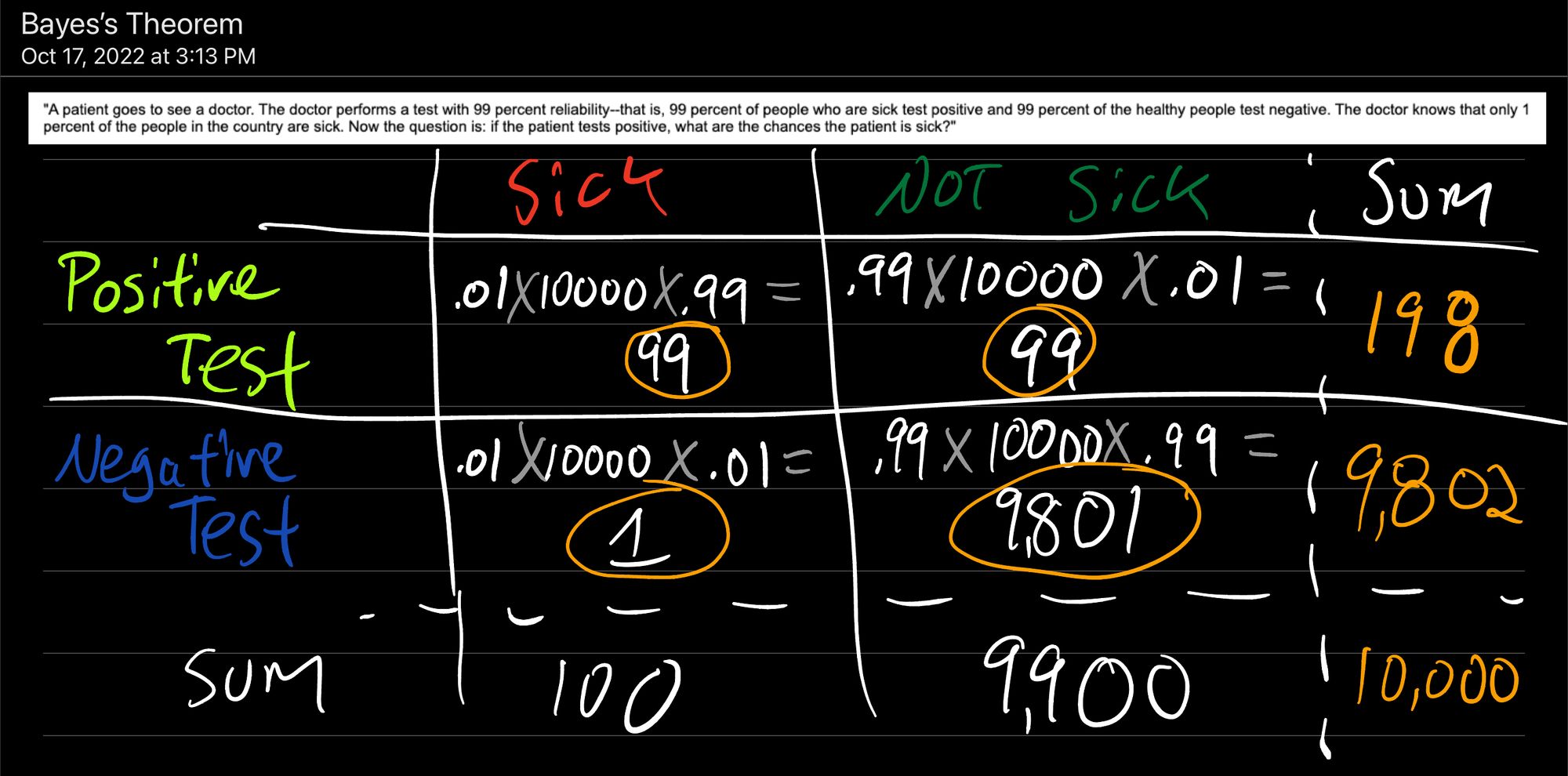
The chart above details the likelihood that a Positive Test identifies a Sick person:

0.01 [percentage of people in the population who are sick] x 10,000 [number of people in our population] x 0.99 [the test is 99% accurate at identifying Sick people with a Positive Test] = 99 people identified with a Positive Test who were actually Sick

Likewise for a Positive Test identifying someone who is Not Sick:

0.99 [percentage of people in the population who are Not Sick] x 10,000 [number of people in our population] x .01 [1% of the time, the test fails and identifies someone who is Not Sick as Positive] = 99 people identified with Positive Test who were Not Sick

Negative Test identifying someone who is Sick:

0.01 [percentage of people in the population who are Sick] x 10,000 [number of people in our population] x .01 [1% of the time, the test fails and identifies someone who is Sick as Negative] = 1 person identified with Negative Test who was Sick

Negative Test identifying someone who is Not Sick:

0.99 [percentage of people in the population who are Not Sick] x 10,000 [number of people in our population] x .99 [the test is 99% accurate at identifying Not Sick people with a Negative Test] = 9,900 people identified with Negative Test who were Not Sick

Back to Bayes' Theorem:

We want to know P(A|B) or the probability someone is Sick (A) given that the patient has a Positive Test (B)

Thus P(Sick | Positive Test) = P(Positive Test | Sick) * P(Sick) / P(Positive Test)

We know P(Sick) = 0.01 [1% of the population is sick]

We know that P(Positive Test | Sick) = 0.99 [99% of the time, the test correctly identifies someone who is Sick with a Positive Test]

And we know that P(Positive Test) = 198/10,000 [from our chart above only 198 in 10,000 people will get a Positive Test] = .0198

Thus P(Sick | Positive Test) = 0.5 = 50%

In this example with the 99% effective test, if you test positive, you have only a 50%(!!) chance of actually being sick.

What Have We Learned?

A 99% effective test is not good enough to elucidate meaningful information from a population that is only 1% infected.

"If X medicine increases your chance of avoiding disease by 30% then why wouldn't you take the 30% increase in your health?"

Likewise, a 30% increase in my chance of avoiding some disease is meaningless without knowing what my chance was of getting the disease beforehand.

If I was 100% likely to get the disease, a 30% reduction would be amazing.

If I'm only 50% likely to get the disease, a 30% reduction is still great - it brings me down to 35% likely to get the disease.

If, however, I only have a 1 in 10,000 (.0001 or .01%) chance of getting the disease a 30% reduction stops being as meaningful.

It brings me down to about 1 in 14,285 (0.00007 or 0.007%).

If you asked me if I'd like to reduce my risk of infection from 1 in 10,000 to 1 in 14,285, all of a sudden the medicine seems a lot less necessary.

TLDR;

Relative rates matter.

If someone tells you that you're going to get a 70% reduction or be 100% more likely to blah blah blah you ALWAYS have to ask yourself:

"What was my chance of this thing happening in the first place?"

If you were 1 in 100,000 to get some disease, it's probably not worth undergoing an expensive or risky treatment even if it makes your odds decrease to 1 in 300,000

Likewise, if you were 1 in 100,000 to get some disease and if you don't stop eating your favorite donuts your risk will increase 100% to 1 in 50,000 - it's probably fine to just keep eating the donuts

If none of this made sense, this video does a really good job of explaining the concept